티스토리 뷰
하... 까딱하면
과제가 너무 어렵습니다 선생님
라고 할 뻔했습니다.
...
오히려 좋아 마인드 장착하겠습니다.

감사합니다. 덕분에 팔자에도 없던 골드 문제들을 풀어봅니다.이때까진 몰랐다. 그 다음 문제가 더 어렵다는 것을.
문제 설명
https://www.acmicpc.net/problem/2110
저의 사랑 (이)도현 씨의 집이 수직선 위에 있다고 합니다. 집이 여러 채라니... 그는 재력마저 갖춘 것을 알 수 있습니다.
그의 집에 공유기를 설치할 건데, 가장 인접한 두 공유기 사이의 거리를 최대로 하고 싶은 겁니다.
- 입력으로 집의 개수 N, 공유기 개수 C와 N개의 집의 좌표 xi가 주어집니다.
- 2 ≤ N ≤ 200,000
- 2 ≤ C ≤ N
- 0 ≤ xi ≤ 1,000,000,000
- 한 집에는 하나의 공유기만 설치 가능합니다.
입력 예시
5 3
1
2
8
4
93- 집 5채 중에 3곳에 공유기를 설치할 건데, 이때 어떤 집에 설치하느냐에 따라 공유기 사이의 거리가 달라집니다.
- 설치한 3개 중 가장 인접한 두 공유기 사이의 거리가 최대여야 하기 때문에, 이 예시의 경우 1,4,9번 집에 설치하면 됩니다.
- 1번과 4번이 가장 인접해 있고 이 둘의 거리가 3이기 때문에 3을 출력합니다.
풀이 과정


백준 풀다가 인생이 다 간다는 소리가 괜히 있는 게 아닌 것 같습니다.
며칠간 골드 문제를 풀면서 든 생각은 저는 예외사항 처리? 를 잘 못 하는 것 같습니다.
풀이의 핵심 아이디어는 나름 생각해내도 구현 과정에서 철저하지 못 한 것 같습니다.
왜냐하면 맨 처음 제출한 코드와 1시간을 수정해서 제출한 코드가 그리 다르지가 않습니다.
하.하.하 아니면 대부분이 이런가요?
일단 집을 탐색해야겠는데, xi의 범위가 엄청나기 때문에 완전탐색은 아닐 테니 이번 주가 이분탐색이니까 이분탐색일 겁니다.
이분탐색을 어떻게 적용해야 할까요?
1) 이분탐색의 기준 값 설정하기
문제에서 원하는 값이 '공유기 사이의 거리'이기 때문에 이 값을 기준으로 이분탐색을 시도하면 될 것 같습니다.
2) 이분탐색을 위한 값의 최소, 최대 설정하기
공유기 사이의 가능한 최소 거리는 1로, 최대 거리는 max(xi) - min(xi)로 설정합니다.
3) 범위 반절씩 줄여가며 이분탐색 Let's go
이 3번이 가장 어려웠습니다.
우선 아이디어는 다음과 같습니다.
공유기를 설치할 거리를 이분탐색을 통해 좁혀나갈 거야.
수직선의 제일 왼쪽 집부터 차례대로 공유기를 설치할 거야.
일단 처음 distance 값(최대 + 최소를 반으로 나눈 값 즉, 중간값!) 만큼 띄워서 수직선의 왼쪽 집부터 설치해봐.
냅다 distance씩 띄워서 설치했는데? 설치해야 하는 공유기의 개수 C개보다 작아.
그렇다는 건 공유기를 너무 띄워서 설치했다는 말이지. 간격을 좁히면 더 많은 공유기를 설치할 수 있을 거야. -> mid의 왼쪽 범위 채택.
냅다 distance씩 띄워서 설치했는데? 설치해야 하는 공유기의 개수 C개보다 커.
그렇다는 건 공유기를 너무 붙여서 설치했다는 말이지. 간격을 넓히면 더 적은 공유기를 설치하게 될 거야. -> mid의 오른쪽 범위 채택.
근데 설치해야 하는 공유기의 개수 C개와 같다면? 어 이 거리다. 하고 끝내야 할까?
응 아닙니다.
전형적인 이분탐색 문제들은 여기서 break를 해서 빠져나가 끝나는데요.
여기서 우리는 인접 거리의 하한을 distance로 정한 것이기 때문에, (물론 현재 distance 값도 유효하지만!) distance보다 넓은 간격으로 공유기를 설치해도 C개와 같을 가능성이 남아 있게 됩니다. 문제는 최대 거리를 원하기 때문에 더 확인해 봐야 합니다.
# 입력
N, C = map(int, input().split())
# 집들의 좌표 입력 받고 오름차순 정렬
house_coordinates = sorted([int(input()) for _ in range(N)])
# 이분탐색의 범위 설정
min_distance = 1
max_distance = house_coordinates[N-1] - house_coordinates[0]
# 범위를 벗어나지 않는 한 반복
while min_distance <= max_distance:
# 중간값 설정
distance = (min_distance + max_distance) // 2
# 공유기 개수 -> 공유기를 1번 집에 설치하고 시작하기 때문에 1로 초기화
sharing_count = 1
# 직전에 공유기가 설치된 집의 인덱스 값 -> 1번 집에 설치했기 때문에 인덱스 0으로 초기화
before_sharing_idx = 0
# 집 좌표 순회
for i in range(1, N):
# 현재 좌표가 공유기가 설치된 집으로부터 distance 이상 떨어진 거리에 있는 집이라면 -> 현재 좌표에 공유기 설치
if house_coordinates[i] >= house_coordinates[before_sharing_idx] + distance:
# 공유기 카운트 증가
sharing_count += 1
# 인덱스 값 i로 업데이트
before_sharing_idx = i
# 공유기 개수가 도현씨가 원하는 C와 같아졌다면
if sharing_count == C:
# for 문을 탈출하여 집 좌표 순회는 종료
break
# distance 기준으로 공유기를 설치해본 결과, 설치된 공유기의 개수가 C개 이상이라면 -> 사이 거리가 너무 작음
# => 더 넓게 설치해보자
if sharing_count >= C:
# 거리의 최솟값을 키운다 즉 distance 기준 오른쪽 범위를 취하여 다시 확인한다
min_distance = distance + 1
# distance 기준으로 공유기를 설치해본 결과, 설치된 공유기의 개수가 C개보다 적다면 -> 사이 거리가 너무 큼
# => 더 좁게 설치해보자
else:
# 거리의 최댓값을 줄인다 즉 distance 기준 왼쪽 범위를 취하여 다시 확인한다
max_distance = distance - 1
# 찾은 거리 중 최댓값을 출력
print(max_distance)그래서 위의 코드와 같이 distance로 C개를 찾았을 때에도 C개 이상 찾은 것과 똑같이 거리의 최솟값을 distance보다 한 칸 크게 잡아서 간격을 넓혀 다시 확인하게 됩니다.
그러다가 while 문의 조건을 만족하지 못 하게 되면 끝나는데, 이 때 C개를 설치할 수 있는 거리 중 가장 큰 값이 max_distance에 남게 되기 때문에 이를 출력해야 문제가 원하는 인접 거리의 최댓값이 됩니다.
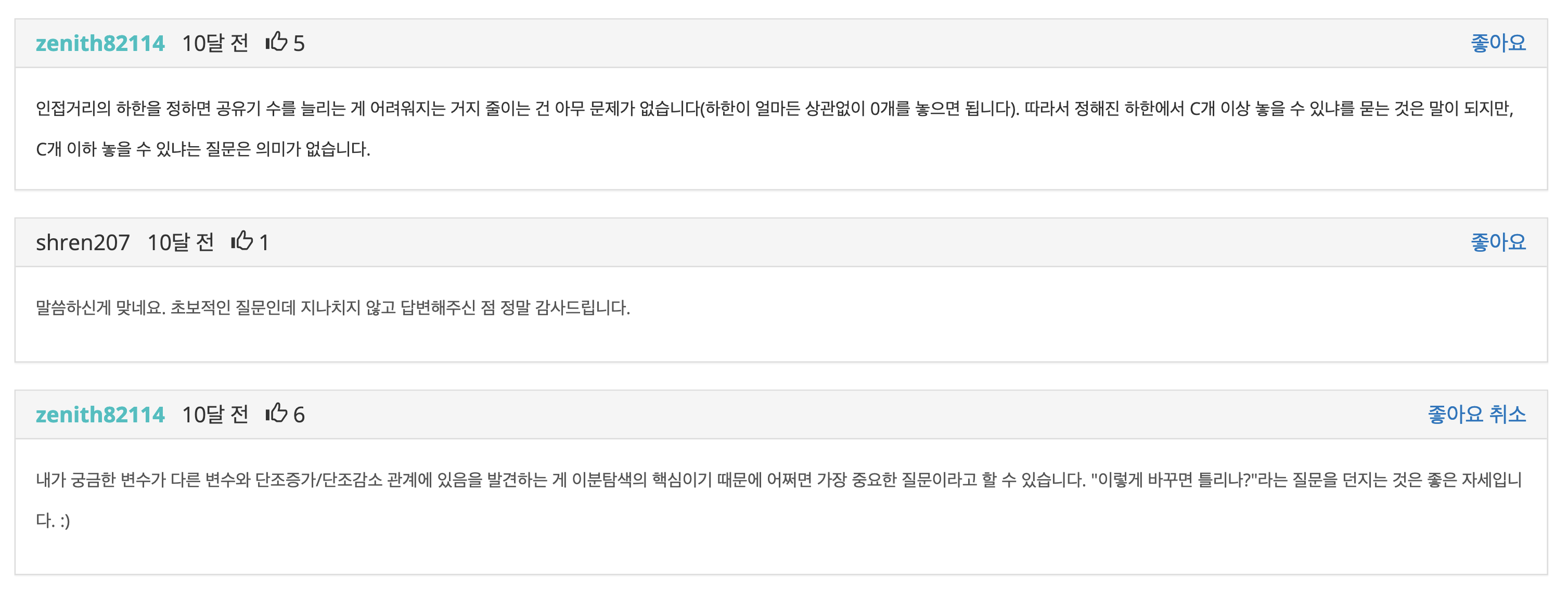
질문 게시판 보다가 너무 좋은 글이 있어서 가져와 봤습니다.
'내가 궁금한 변수가 다른 변수와 단조증가/단소감소 관계에 있다' 라는 것은 변수 하나가 변할 때 다른 변수가 일정하게 증가하거나 감소하는 관계를 뜻합니다.
이 문제도 인접한 집들의 최소 거리를 설정했을 때,
최소 거리가 커질수록 -> 설치 가능한 공유기의 개수가 줄어들고
최소 거리가 작아질수록 -> 설치 가능한 공유기의 개수가 증가하는 관계입니다.
이분탐색은 '어느 조건 이상일 때 결과가 참'이라는 구조에서 사용됩니다.
예를 들어, 어떤 값 X가 증가할수록 조건을 만족하지 않게 된다면, X를 기준으로 어디까지 참이었는지를 탐색하게 되고,
이 때 단조증가/단조감소 관계가 존재하기 때문에 탐색할 범위를 절반으로 줄이면서 조건을 확인할 수 있는 것이 이분탐색의 핵심이 됩니다.
by. GPT 선생님
이분탐색? 슬슬 알 것 같기도 하고... (유언)
이상입니다.
'Algorithm' 카테고리의 다른 글
| 백준 1904번: 01타일 (S3) - Python 풀이 (0) | 2025.02.22 |
|---|---|
| 백준 1939번: 중량제한 (G3) - Python 풀이 (0) | 2025.02.18 |
| 프로그래머스 Lv.3: 퍼즐 조각 채우기 - Python 풀이 X 정답 이해 O (0) | 2025.02.16 |
| 백준 3079번: 입국심사 (G5) - Python 풀이 (1) | 2025.02.14 |
| 백준 2606번: 바이러스 (S3) - Python 풀이 (0) | 2025.02.08 |
- Total
- Today
- Yesterday
- 그리디
- MySQL
- 큐
- 알고리즘
- 다이나믹프로그래밍
- 자료구조
- 백준
- 프로그래머스
- Dijkstra
- Swift로백준풀기
- 힙
- 해시
- 스택
- Baekjoon
- 투포인터
- 코테준비
- 그래프
- ios
- 코딩테스트
- 구현
- ios앱개발
- 이분탐색
- dp
- 다익스트라
- Python
- Swift
- 정렬
- SQL
- Programmers
- 코테
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |

